CONIC SECTIONS PROJECT
Algebra II Topic: Conics
By: Avra, Natalie, Brooke, Riley and Jasper
Conics Definition:
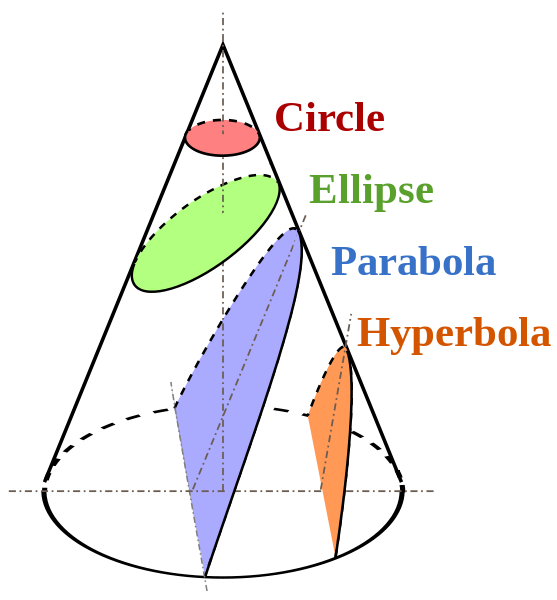
In Algebra II, the concept of a conic section or simply conics is a geometrical equation for a curve that is formed when a plane intersects a double napped cone; this includes circles, ellipses, parabolas and hyperbolas.
"Conics." - Maths Accelerator. Web. 28 Apr. 2013. <http://www.mathsaccelerator.com/algebra/conics>.
Conics is where you create a double napped cone, which is a hollow object made of lines that narrow and fall from a circular base to join at a point, and then extend infinitely in both directions. To then create the conic section, a plane can intersect any part of the double napped cone to create either a circle, an ellipse, a parabola, or a hyperbola. An ellipse would be formed by placing a plane vertically in any part of either cone without touching the other one, and is when “all points [are] found by keeping the sum of the distances from two points (each of which is called a focus of the ellipse) constant” (http://www.algebralab.org/lessons/lesson.aspx?file=Algebra_conics_ellipse.xml). An ellipse forms an oval shape. A circle is a line forming a loop that closes, where all points on the line are of equal distance from a point in the center. It is another conic which originates from the ellipse. In order to create a circle, a plane would need to be placed either above or below the apex (the point where the two cones come to one point) and would be parallel to the apex plane. The plane would have to intersect in such a way to create a circle that has an equidistant radius at all points of the circumference of the circle. A circle is a line forming a loop that closes, where all points on the line are of equal distance from a point in the center. To make a parabola, a plane would be positioned at an angle to where it would be parallel to the other double napped cone. This would generate a straight line in the cone it’s held in. A hyperbola, is a smooth curve created by a plane and is created through the intersection of a double napped cone that intersect the cones at both ends of the apex. A hyperbola always has two pieces two it that our connected by the plane and are symmetric to each other.
How to Learn About Conics:
In order to learn the concept of conics, a couple of things are required. Some of the concepts you should already have an understanding of before beginning to use conics are being able to graph quadratic functions, solving linear systems, and completing the square. You should be confident in these concepts so that you may learn how to write an equation for a conic section. Understanding how to graph may be the most important skill to learn. Many of these concepts can be learned in Geometry, Algebra One, and Algebra Two. Geometry introduces you to simple equations and graphing circles and ellipses as well as reviews the relations between points, lines, and surfaces. Algebra 1 is also recommended because you are introduced to graphing parabolas. In Algebra 2 you gain an understanding of graphing hyperbolas and have more knowledge in graphing complex equations. Another very important thing is understanding the different shapes and equations for graphing. Although parabolas, circles, ellipses, and hyperbolas are all a part of Conic Sections, they all have different shapes and equations to graph them. here are the equations:
Circle
x2 +y2=r2
x2/a2 + y2/b2 = 1
Ellipse
(x-h)2+(y-k)2=r2
(x-h)2/a2 + (y-k)2/b2 = 1
Parabola
x2=4py
(y-k)2=4p(x-h)
Hyperbola
x2/a2-y2/b2=1
(x-h)2/a2 – (y-k)2/b2 = 1 or
(x-h)2/a2+(y-k)2/b2 = 1
These equations should help get you started with graphing your own conics. Lastly, vocabulary is another thing that you should learn. These can help clarify the different parts of the conic shapes.
Professions that use Conics:
There are many professions that utilize Conic Sections in their daily lives. From headlamps on cars to the rendering of a proposed interior design plan for a new house, Conics can play an integral role in the creation and support of these ideas.
Other professions that utilize Conics include:
-Architects
-Astronomers
-Car Manufacturers
-Digital Designers
-Interior Designers
-Cake Industries (like wedding cakes)
-Flashlight and Light Bulb Manufacturers
-Computer Software Engineers
-Nuclear Engineers
-Mechanical Engineers
-Aerospace Engineers
-Environmental Engineers
-Agricultural Managers
-Astrophysics
-Math Teachers
-Weapons testing
-Pyrotechnicians
-3D Animators
Examples Of Conics In Professions:
An Example of Conics in Astronomy:
“According to Kepler's First Law of Planetary Motion, the orbit of each planet is an ellipse, with one focus of that ellipse at the center of the Sun. Newton's reformulation of this Law states that the orbit of each planet is a conic section, with one focus of that conic section at the center of the Sun. To properly understand planetary orbits, we therefore need some understanding of ellipses in particular, and conic sections in general”. (http://cseligman.com/text/history/ellipses.htm).
Comets
"It can be proved, using calculus and elementary physics, that the orbit of a comet or an asteroid is always a conic section. The eccentricity of a comet can indicate the total energy of the comet. Roughly speaking, the faster the comet travels, the greater its eccentricity. Thus, for example, a slow-moving comet (relatively speaking) has eccentricity less than 1 and travels in an ellipse. When the comet travels at precisely the correct speed, its eccentricity becomes 1 and its orbit changes to a parabola. If the comet is moving faster still, its eccentricity is greater than 1 and its orbit is a hyperbola” (http://conicsections.freehomepage.com/).
Example Problem Orbiting the earth
The eccentricity of the earth's orbit about the sun is approximately 0.0167. The closest distance between the earth and the sun is approximately 93 million miles. What is the furthest distance between the earth and the sun? (See Figure 1.)
Solution
Let a be the semimajor axis of the orbit. Assume that the center of the ellipse is (0, 0). Suppose that the sun is at the focus (c, 0). Then:
a - c = 93
a = c + 93
Therefore:
The furthest distance of the earth from the sun is a + c = 2c + 93. Therefore, a + c = 2c + 93 = 96.159 million miles.
(http://conicsections.freehomepage.com/)
Example of Conics in Car Manufacturing:
Car designers use Conics to create parabolas in the design of car headlights and in high beams because it aids in concentrating the light beam. The focus of a parabola has an important property when constructing headlamps on cars. The surface of an automobile headlamp is reflective surface which is parabolic. The actual halogen light bulb is then placed at the focus and the light then reflects off this surface in “parallel” beams which then focus the the light directly in front of the car. This occurs because any light source at the focus of a parabola reflects its beams parallel to the axis of symmetry of the parabola. The parabolic mirror therefore directs the energy arriving over its surface to a 'hot spot' at the focus.
"Conic Sections: Focus and Directrix." Conic Sections: Focus and Directrix. Web. 28 Apr. 2013. <http://www.algebralab.org/lessons/lesson.aspx?file=Algebra_conics_directrix.xml>.
The basic shape of a parabola is derived from the equation: y² = 4ax [1]
Parabolic reflectors are used to collect energy from a distant source and bring it to a common focal point, thus correcting spherical aberration found in simpler spherical reflectors. Since the principles of reflection are reversible, parabolic reflectors can also be used to project energy of a source at its focus outward in a parallel beam, used in devices such as spotlights and car headlights. Parabolic reflectors have the property that the light rays or sound waves coming parallel to its axis converge at the focus and then it reflects them parallel to the axis.
If a parabolic reflector is 20 cm in diameter and 5 cm deep, find its focus.
Solution: Let LAM be the parabolic reflector such that LM is its diameter and AN is its depth. It is given that AN = 5 cm and LM = 20 cm
LN = NM = 10 cm.
Taking A as the origin, AX along x- axis and a line through A perpendicular to AX as y-axis, let the equation of the reflector be
y2 = 4ax
The coordinates of L(5,10) lies on the parabola .Therefore,
102 = 4a*5 `=>` 100 = 20a `=>` a = 5
So, the equation of the reflector is
y2 = 20x
Its focus is at (5,0) i.e. at point N.
Citation for This Example Problem:
"Parabola Word Problems - Revise Math." Parabola Word Problems - Revise Math. Web. 19 Apr. 2013. <http://revisemath.jimdo.com/geometry/parabola-word-problems/>.
"Parabolic Reflector." Wikipedia. Wikimedia Foundation, 25 Apr. 2013. Web. 28 Apr. 2013. <http://en.wikipedia.org/wiki/Parabolic_reflector>.
Example of Conics in Bridge Engineering:
Our approach to this problem was to use a photo we had taken of the bridge, and by making measurements on the photo in pixel units, (using Adobe Fireworks), scale the photo and obtain some (x,y) values to work with.
The “Scale Factor” was derived by knowing that the real life span distance of the roadway below the arch was 503 meters, and then comparing this with the number of pixels (or dots) on the photo for this span.
As shown above, this enabled us to then establish the following key values:
Vertex Turning point is located at (h,k) = (251.5, 118)
Three other (x,y) points on the arch are: (323,108) and (394.5,80) and (503,0).
For any inverted Parabola graph, there is a standard equation that uses the (h,k) vertex, and the “Dilation Factor” of “a”, to determine the value of any (x,y) point on the Parabola graph.
The “Dilation Factor” value relates to how much the standard y = x squared parabola shape has been stretched or compressed.
This standard quadratic equation is as follows:
Image Copyright 2012 by Passy’s World of Mathematics
For the Bridge, we have the vertex value, and we have some (x,y) values, and so all we need to do is determine the “a” Dilation Factor value.
This can be done as shown below:
Image Copyright 2012 by Passy’s World of Mathematics
Substituting back into the standard equation, we then have the equation for the lower arch of the Bridge as the following:
Image Copyright 2012 by Passy’s World of Mathematics
Note that we have rounded off the Dilation Factor (“a” value) in our Equation to be 0.00188. This means in subsequent checking activities which follow, we did have to round off or truncate some “Y” values.
For better accuracy, the exact value of a = 0.001880501 can be used.
Source:http://passyworldofmathematics.com/sydney-harbour-bridge-mathematics/
Another Example of Conics In Bridge Engineering:
One particular profession that uses conics in their everyday routine is an architect. There are multiple examples of buildings that include conics in their structure. One unusual example of architecture is using conics in bridges. Possibly the most famous bridge in the United States, the Golden Gate Bridge is a perfect example for a parabolic equation.
Assuming the vertex is (0,0), we can start graphing our parabola, but not before knowing some crucial specifications.
Height of tower above water:
746 ft = 227 m
Height of tower above the road:
500 ft = 152 m
Length of side span:
1,125 ft = 343 m
Since the vertex of the parabola (0,0) is on the road, at the center of the span, the point at the top of the tower has the coordinates of (343,152). Now all we have to do, is substitute the coordinates of point (343,152) into x2 = 4ay and solve for a.
3432=4a(152)
117,649=4a(152)
117,649/4=a(152)/4
29,412.25=(152)a
29,412.25/152=a/152
a=193.5
Bibliography:
"7 Conics." 7 Conics. Web. 28 Apr. 2013. <http://www.geom.uiuc.edu/docs/reference/CRC-formulas/node26.html>.
"8.1 - Conics." 8.1 - Conics. Web. 28 Apr. 2013. <http://people.richland.edu/james/lecture/m116/conics/conics.html>.
"Calculation of an Orbit from Three Observations." Calculation of an Orbit from Three Observations. Web. 28 Apr. 2013. <http://science.larouchepac.com/gauss/ceres/InterimII/Astronomy/KeplerProblem.html>.
"Conic Section." - Geometry. Web. 28 Apr. 2013. <http://www.icoachmath.com/math_dictionary/conic_section.html>.
"Conic Section Applications: Parabolas." Prezi.com. Web. 28 Apr. 2013. <http://prezi.com/hktby0lfibaz/conic-section-applications-parabolas/>.
"Conic Section." Wikipedia. Wikimedia Foundation, 28 Apr. 2013. Web. 28 Apr. 2013. <http://en.wikipedia.org/wiki/Conic_section>.
"Conic Sections." - Circles, Ellipses, Parabolas, and Hyperbolas. Web. 28 Apr. 2013. <http://www.wyzant.com/help/math/algebra/conic_sections>.
"Conic Sections: Ellipses." Conic Sections: Ellipses.Web. 28 Apr. 2013. <http://www.algebralab.org/lessons/lesson.aspx?file=Algebra_conics_ellipse.xml>.
"Conics." - Maths Accelerator. Web. 28 Apr. 2013. <http://www.mathsaccelerator.com/algebra/conics>.
"Conics: An Overview." Conics: An Overview. Web. 28 Apr. 2013. <http://www.purplemath.com/modules/conics.htm>.
"The Conics." The Conics. Web. 28 Apr. 2013. <http://mathforum.org/sanders/geometry/GP16Conics.html>.
"Definition:Cone." - ProofWiki. Web. 28 Apr. 2013. <http://www.proofwiki.org/wiki/Definition:Cone>.
"Definition:Cone." - ProofWiki. Web. 28 Apr. 2013. <http://www.proofwiki.org/wiki/Definition:Cone>.
"The Geometry of the Conic Sections." The Geometry of the Conic Sections. Web. 28 Apr. 2013. <http://rowdy.mscd.edu/~talmanl/HTML/GeometryOfConicSections.html>.
"Hey Visitor!" Ted's WAC Book for Math. Web. 28 Apr. 2013. <http://tpanitz.jimdo.com/ted-s-wac-book-for-math/>.
Hui, T. L. "XP Math - Jobs That Use." XP Math - Jobs That Use. N.p., n.d. Web. 30 Apr. 2013. <http://www.xpmath.com/careers/topicsresult.php?subjectID=4>.
"Loftsman." Loftsman. Web. 28 Apr. 2013. <http://www.melmoth2.com/texts/Lofting.htm>.
"Math2.org Math Tables: Conic Sections." Conic Sections. Web. 28 Apr. 2013. <http://math2.org/math/algebra/conics.htm>.
"Occurrence of the Conics." Occurrence of the Conics. Web. 28 Apr. 2013. <http://britton.disted.camosun.bc.ca/jbconics.htm>.
"Parabolic Reflector." Wikipedia. Wikimedia Foundation, 25 Apr. 2013. Web. 28 Apr. 2013. <http://en.wikipedia.org/wiki/Parabolic_reflector>.
"Towson University." Towson University. Web. 28 Apr. 2013. <http://www.towson.edu/>.
"University of Florida College of Engineering." Wikipedia. Wikimedia Foundation, 28 Apr. 2013. Web. 28 Apr. 2013. <http://en.wikipedia.org/wiki/University_of_Florida_College_of_Engineering>.
Conics Definition:
In Algebra II, the concept of a conic section or simply conics is a geometrical equation for a curve that is formed when a plane intersects a double napped cone; this includes circles, ellipses, parabolas and hyperbolas.
"Conics." - Maths Accelerator. Web. 28 Apr. 2013. <http://www.mathsaccelerator.com/algebra/conics>.
Conics is where you create a double napped cone, which is a hollow object made of lines that narrow and fall from a circular base to join at a point, and then extend infinitely in both directions. To then create the conic section, a plane can intersect any part of the double napped cone to create either a circle, an ellipse, a parabola, or a hyperbola. An ellipse would be formed by placing a plane vertically in any part of either cone without touching the other one, and is when “all points [are] found by keeping the sum of the distances from two points (each of which is called a focus of the ellipse) constant” (http://www.algebralab.org/lessons/lesson.aspx?file=Algebra_conics_ellipse.xml). An ellipse forms an oval shape. A circle is a line forming a loop that closes, where all points on the line are of equal distance from a point in the center. It is another conic which originates from the ellipse. In order to create a circle, a plane would need to be placed either above or below the apex (the point where the two cones come to one point) and would be parallel to the apex plane. The plane would have to intersect in such a way to create a circle that has an equidistant radius at all points of the circumference of the circle. A circle is a line forming a loop that closes, where all points on the line are of equal distance from a point in the center. To make a parabola, a plane would be positioned at an angle to where it would be parallel to the other double napped cone. This would generate a straight line in the cone it’s held in. A hyperbola, is a smooth curve created by a plane and is created through the intersection of a double napped cone that intersect the cones at both ends of the apex. A hyperbola always has two pieces two it that our connected by the plane and are symmetric to each other.
How to Learn About Conics:
In order to learn the concept of conics, a couple of things are required. Some of the concepts you should already have an understanding of before beginning to use conics are being able to graph quadratic functions, solving linear systems, and completing the square. You should be confident in these concepts so that you may learn how to write an equation for a conic section. Understanding how to graph may be the most important skill to learn. Many of these concepts can be learned in Geometry, Algebra One, and Algebra Two. Geometry introduces you to simple equations and graphing circles and ellipses as well as reviews the relations between points, lines, and surfaces. Algebra 1 is also recommended because you are introduced to graphing parabolas. In Algebra 2 you gain an understanding of graphing hyperbolas and have more knowledge in graphing complex equations. Another very important thing is understanding the different shapes and equations for graphing. Although parabolas, circles, ellipses, and hyperbolas are all a part of Conic Sections, they all have different shapes and equations to graph them. here are the equations:
Circle
x2 +y2=r2
x2/a2 + y2/b2 = 1
Ellipse
(x-h)2+(y-k)2=r2
(x-h)2/a2 + (y-k)2/b2 = 1
Parabola
x2=4py
(y-k)2=4p(x-h)
Hyperbola
x2/a2-y2/b2=1
(x-h)2/a2 – (y-k)2/b2 = 1 or
(x-h)2/a2+(y-k)2/b2 = 1
These equations should help get you started with graphing your own conics. Lastly, vocabulary is another thing that you should learn. These can help clarify the different parts of the conic shapes.
- center: the point (h, k) at the center of a circle, an ellipse, or a hyperbola.
- vertex: in the case of a parabola, the point (h, k) at the "end" of a parabola; in the case of an ellipse, an end of the major axis; in the case of a hyperbola, the turning point of a branch of a hyperbola; the plural form is "vertices" (VUR-tuh-seez).
- focus: a point from which distances are measured in forming a conic; a point at which these distance-lines converge, or "focus"; the plural form is "foci".
- directrix: a line from which distances are measured in forming a conic; the plural form is "directrices".
- axis: a line perpendicular to the directrix passing through the vertex of a parabola; also called the "axis of symmetry"; the plural form is "axes”.
- major axis: a line segment perpendicular to the directrix of an ellipse and passing through the foci; the line segment terminates on the ellipse at either end; also called the "principal axis of symmetry"; the half of the major axis between the center and the vertex is the semi-major axis.
- minor axis: a line segment perpendicular to and bisecting the major axis of an ellipse; the segment terminates on the ellipse at either end; the half of the minor axis between the center and the ellipse is the semi-minor axis.
- locus: a set of points satisfying some condition or set of conditions; each of the conics is a locus of points that obeys some sort of rule or rules; the plural form is "loci".
Professions that use Conics:
There are many professions that utilize Conic Sections in their daily lives. From headlamps on cars to the rendering of a proposed interior design plan for a new house, Conics can play an integral role in the creation and support of these ideas.
Other professions that utilize Conics include:
-Architects
-Astronomers
-Car Manufacturers
-Digital Designers
-Interior Designers
-Cake Industries (like wedding cakes)
-Flashlight and Light Bulb Manufacturers
-Computer Software Engineers
-Nuclear Engineers
-Mechanical Engineers
-Aerospace Engineers
-Environmental Engineers
-Agricultural Managers
-Astrophysics
-Math Teachers
-Weapons testing
-Pyrotechnicians
-3D Animators
Examples Of Conics In Professions:
An Example of Conics in Astronomy:
“According to Kepler's First Law of Planetary Motion, the orbit of each planet is an ellipse, with one focus of that ellipse at the center of the Sun. Newton's reformulation of this Law states that the orbit of each planet is a conic section, with one focus of that conic section at the center of the Sun. To properly understand planetary orbits, we therefore need some understanding of ellipses in particular, and conic sections in general”. (http://cseligman.com/text/history/ellipses.htm).
Comets
"It can be proved, using calculus and elementary physics, that the orbit of a comet or an asteroid is always a conic section. The eccentricity of a comet can indicate the total energy of the comet. Roughly speaking, the faster the comet travels, the greater its eccentricity. Thus, for example, a slow-moving comet (relatively speaking) has eccentricity less than 1 and travels in an ellipse. When the comet travels at precisely the correct speed, its eccentricity becomes 1 and its orbit changes to a parabola. If the comet is moving faster still, its eccentricity is greater than 1 and its orbit is a hyperbola” (http://conicsections.freehomepage.com/).
Example Problem Orbiting the earth
The eccentricity of the earth's orbit about the sun is approximately 0.0167. The closest distance between the earth and the sun is approximately 93 million miles. What is the furthest distance between the earth and the sun? (See Figure 1.)
Solution
Let a be the semimajor axis of the orbit. Assume that the center of the ellipse is (0, 0). Suppose that the sun is at the focus (c, 0). Then:
a - c = 93
a = c + 93
Therefore:
The furthest distance of the earth from the sun is a + c = 2c + 93. Therefore, a + c = 2c + 93 = 96.159 million miles.
(http://conicsections.freehomepage.com/)
Example of Conics in Car Manufacturing:
Car designers use Conics to create parabolas in the design of car headlights and in high beams because it aids in concentrating the light beam. The focus of a parabola has an important property when constructing headlamps on cars. The surface of an automobile headlamp is reflective surface which is parabolic. The actual halogen light bulb is then placed at the focus and the light then reflects off this surface in “parallel” beams which then focus the the light directly in front of the car. This occurs because any light source at the focus of a parabola reflects its beams parallel to the axis of symmetry of the parabola. The parabolic mirror therefore directs the energy arriving over its surface to a 'hot spot' at the focus.
"Conic Sections: Focus and Directrix." Conic Sections: Focus and Directrix. Web. 28 Apr. 2013. <http://www.algebralab.org/lessons/lesson.aspx?file=Algebra_conics_directrix.xml>.
The basic shape of a parabola is derived from the equation: y² = 4ax [1]
Parabolic reflectors are used to collect energy from a distant source and bring it to a common focal point, thus correcting spherical aberration found in simpler spherical reflectors. Since the principles of reflection are reversible, parabolic reflectors can also be used to project energy of a source at its focus outward in a parallel beam, used in devices such as spotlights and car headlights. Parabolic reflectors have the property that the light rays or sound waves coming parallel to its axis converge at the focus and then it reflects them parallel to the axis.
If a parabolic reflector is 20 cm in diameter and 5 cm deep, find its focus.
Solution: Let LAM be the parabolic reflector such that LM is its diameter and AN is its depth. It is given that AN = 5 cm and LM = 20 cm
LN = NM = 10 cm.
Taking A as the origin, AX along x- axis and a line through A perpendicular to AX as y-axis, let the equation of the reflector be
y2 = 4ax
The coordinates of L(5,10) lies on the parabola .Therefore,
102 = 4a*5 `=>` 100 = 20a `=>` a = 5
So, the equation of the reflector is
y2 = 20x
Its focus is at (5,0) i.e. at point N.
Citation for This Example Problem:
"Parabola Word Problems - Revise Math." Parabola Word Problems - Revise Math. Web. 19 Apr. 2013. <http://revisemath.jimdo.com/geometry/parabola-word-problems/>.
"Parabolic Reflector." Wikipedia. Wikimedia Foundation, 25 Apr. 2013. Web. 28 Apr. 2013. <http://en.wikipedia.org/wiki/Parabolic_reflector>.
Example of Conics in Bridge Engineering:
Our approach to this problem was to use a photo we had taken of the bridge, and by making measurements on the photo in pixel units, (using Adobe Fireworks), scale the photo and obtain some (x,y) values to work with.
The “Scale Factor” was derived by knowing that the real life span distance of the roadway below the arch was 503 meters, and then comparing this with the number of pixels (or dots) on the photo for this span.
As shown above, this enabled us to then establish the following key values:
Vertex Turning point is located at (h,k) = (251.5, 118)
Three other (x,y) points on the arch are: (323,108) and (394.5,80) and (503,0).
For any inverted Parabola graph, there is a standard equation that uses the (h,k) vertex, and the “Dilation Factor” of “a”, to determine the value of any (x,y) point on the Parabola graph.
The “Dilation Factor” value relates to how much the standard y = x squared parabola shape has been stretched or compressed.
This standard quadratic equation is as follows:
Image Copyright 2012 by Passy’s World of Mathematics
For the Bridge, we have the vertex value, and we have some (x,y) values, and so all we need to do is determine the “a” Dilation Factor value.
This can be done as shown below:
Image Copyright 2012 by Passy’s World of Mathematics
Substituting back into the standard equation, we then have the equation for the lower arch of the Bridge as the following:
Image Copyright 2012 by Passy’s World of Mathematics
Note that we have rounded off the Dilation Factor (“a” value) in our Equation to be 0.00188. This means in subsequent checking activities which follow, we did have to round off or truncate some “Y” values.
For better accuracy, the exact value of a = 0.001880501 can be used.
Source:http://passyworldofmathematics.com/sydney-harbour-bridge-mathematics/
Another Example of Conics In Bridge Engineering:
One particular profession that uses conics in their everyday routine is an architect. There are multiple examples of buildings that include conics in their structure. One unusual example of architecture is using conics in bridges. Possibly the most famous bridge in the United States, the Golden Gate Bridge is a perfect example for a parabolic equation.
Assuming the vertex is (0,0), we can start graphing our parabola, but not before knowing some crucial specifications.
Height of tower above water:
746 ft = 227 m
Height of tower above the road:
500 ft = 152 m
Length of side span:
1,125 ft = 343 m
Since the vertex of the parabola (0,0) is on the road, at the center of the span, the point at the top of the tower has the coordinates of (343,152). Now all we have to do, is substitute the coordinates of point (343,152) into x2 = 4ay and solve for a.
3432=4a(152)
117,649=4a(152)
117,649/4=a(152)/4
29,412.25=(152)a
29,412.25/152=a/152
a=193.5
Bibliography:
"7 Conics." 7 Conics. Web. 28 Apr. 2013. <http://www.geom.uiuc.edu/docs/reference/CRC-formulas/node26.html>.
"8.1 - Conics." 8.1 - Conics. Web. 28 Apr. 2013. <http://people.richland.edu/james/lecture/m116/conics/conics.html>.
"Calculation of an Orbit from Three Observations." Calculation of an Orbit from Three Observations. Web. 28 Apr. 2013. <http://science.larouchepac.com/gauss/ceres/InterimII/Astronomy/KeplerProblem.html>.
"Conic Section." - Geometry. Web. 28 Apr. 2013. <http://www.icoachmath.com/math_dictionary/conic_section.html>.
"Conic Section Applications: Parabolas." Prezi.com. Web. 28 Apr. 2013. <http://prezi.com/hktby0lfibaz/conic-section-applications-parabolas/>.
"Conic Section." Wikipedia. Wikimedia Foundation, 28 Apr. 2013. Web. 28 Apr. 2013. <http://en.wikipedia.org/wiki/Conic_section>.
"Conic Sections." - Circles, Ellipses, Parabolas, and Hyperbolas. Web. 28 Apr. 2013. <http://www.wyzant.com/help/math/algebra/conic_sections>.
"Conic Sections: Ellipses." Conic Sections: Ellipses.Web. 28 Apr. 2013. <http://www.algebralab.org/lessons/lesson.aspx?file=Algebra_conics_ellipse.xml>.
"Conics." - Maths Accelerator. Web. 28 Apr. 2013. <http://www.mathsaccelerator.com/algebra/conics>.
"Conics: An Overview." Conics: An Overview. Web. 28 Apr. 2013. <http://www.purplemath.com/modules/conics.htm>.
"The Conics." The Conics. Web. 28 Apr. 2013. <http://mathforum.org/sanders/geometry/GP16Conics.html>.
"Definition:Cone." - ProofWiki. Web. 28 Apr. 2013. <http://www.proofwiki.org/wiki/Definition:Cone>.
"Definition:Cone." - ProofWiki. Web. 28 Apr. 2013. <http://www.proofwiki.org/wiki/Definition:Cone>.
"The Geometry of the Conic Sections." The Geometry of the Conic Sections. Web. 28 Apr. 2013. <http://rowdy.mscd.edu/~talmanl/HTML/GeometryOfConicSections.html>.
"Hey Visitor!" Ted's WAC Book for Math. Web. 28 Apr. 2013. <http://tpanitz.jimdo.com/ted-s-wac-book-for-math/>.
Hui, T. L. "XP Math - Jobs That Use." XP Math - Jobs That Use. N.p., n.d. Web. 30 Apr. 2013. <http://www.xpmath.com/careers/topicsresult.php?subjectID=4>.
"Loftsman." Loftsman. Web. 28 Apr. 2013. <http://www.melmoth2.com/texts/Lofting.htm>.
"Math2.org Math Tables: Conic Sections." Conic Sections. Web. 28 Apr. 2013. <http://math2.org/math/algebra/conics.htm>.
"Occurrence of the Conics." Occurrence of the Conics. Web. 28 Apr. 2013. <http://britton.disted.camosun.bc.ca/jbconics.htm>.
"Parabolic Reflector." Wikipedia. Wikimedia Foundation, 25 Apr. 2013. Web. 28 Apr. 2013. <http://en.wikipedia.org/wiki/Parabolic_reflector>.
"Towson University." Towson University. Web. 28 Apr. 2013. <http://www.towson.edu/>.
"University of Florida College of Engineering." Wikipedia. Wikimedia Foundation, 28 Apr. 2013. Web. 28 Apr. 2013. <http://en.wikipedia.org/wiki/University_of_Florida_College_of_Engineering>.